30 Years of Credal Networks
Posted on March 24, 2021 by Dennis Mauá and Fabio Cozman (edited by Ignacio Montes)[ go back to blog ]
Abstract
Credal networks combine the intuitive expressivity of graphs and the principled treatment and flexibility of imprecise probability to deliver a powerful framework for uncertainty management. Here, we briefly motivate the use of credal networks, provide a historical account of their development and present a commented bibliography on existing surveys and tutorials on the topic.
An illustrative example
Describing complex phenomena often requires dealing with severe uncertainty, unreliable data, disagreeing opinions, and a large number of interacting factors [PAZ10]. Take as an example the United States National Intelligence report number 29-15, written by a pool of intelligence specialists to inform authorities about the threat of a possible military intervention of the Soviet Union against Yugoslavia in 1951 [Ken14]. A simplified version of the content of the report is captured by the directed acyclic graph of Figure 1, consisting of nodes and arrows. The nodes of the graph represent random variables (in this case, to binary outcomes 1 and 0 representing true and false, respectively). The arrows denote direct influence of a quantity (random variable) on another quantity. For instance, the report stated that a decision to invade by the Soviets depended on a possible regime change in Yugoslavia, that could be caused by Tito’s assassination (the Yugoslav leader), or due to a coup or revolt. We say that the origin of the influence is the parent, and that the receiver of the influence is the child (e.g., attack is a parent of the node invasion, and propaganda is a child of the node decision to invade).
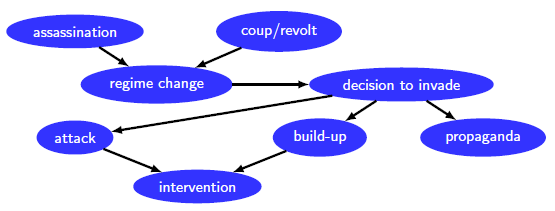
Figure 1. A simplified graphical representation for the reasoning in the 29-51 report.
Bayesian Networks
According to the theory of Bayesian networks, a joint probability distribution (or density) over all random variables is obtained by associating to each node/random variable in the graph a collection of conditional probability distributions, one for each configuration of the values of its parents [Pear88]; [Dar09]; [KF09]. For the model in our example, this would require specifying a distribution \({\mathbb{P}}(\)intervention \(|\) attack\(=a,\)build-up\(=b)\) for \(a,b \in \{ 0,1 \}\), and a distribution \(\mathbb{P}(\)attack\(|\)decision to invade\(=d)\) for \(d \in \{0,1\}\), and so on. From such a joint distribution, we can (in principle) answer any probabilistic query about the variables in the model, such as “What is the probability of an invasion given that we observed a military build-up but no increase in propaganda?”.
Obtaining such a high number of sharp estimates can be quite difficult in practice, and even undesired. For example, the 29-51 report concluded that “an attack […] should be considered a serious possibility”. When asked to quantify such conclusion, the pool of experts could only assert that \(\mathbb{P}(\)attack\() \in [0.2,0.8]\). This type of imprecision in estimates is abundant in practical scenarios, not only when experts are involved, but also when uncertain is gathered from unreliable or scarce data [Wal91].
Credal Networks
By the early 1990’s the need to accommodate imprecise or partial specifications led researchers to develop a theory of credal networks [LM90;CD93]. In short, a credal network is a Bayesian network whose precise probabilities have been imprecisely or partially specified, usually in the form of constraints over probability values, for example, [ \mathbb{P}(\text{attack}!=!1|\text{decision to invade}!=!1)
2\mathbb{P}(\text{attack}!=!1|\text{decision to invade}!=!1) , . ] In fact, Bayesian networks appeared as the result of a long and heated debated during the 1980’s concerning the best way to handle uncertainty [Nil86]; [Qui82]; [SB75]; [Peal88], one that would largely favor a rigorous probabilistic treatment in lieu of ad hoc solutions. Besides allowing for more flexibility in their quantification, the advent of credal networks had a secondary motivation. Researchers interested in artificial intelligence came to realize that many of the alternative proposals to represent uncertainty, from Dempster Shafer theory to possibility theory, could be unified within the general theory of imprecise/indeterminate probability, and credal networks were an excellent modeling tool within that space.
If the ability to represent and reason with imprecision and indeterminacy in probability values allowed credal networks to reach more conservative and robust conclusions than Bayesian networks, it also posed new challenges to researchers. Initially, there was a greater focus on computing which such models, which was essentially meant as obtaining tight bounds on probability values induced by the model. Prominent examples are Cano et al.’s work [CMD93], the 2U’s algorithm by Fagiuoli and Zaffalon [FZ98] and Tessem’s interval propagation [Tes92]. There were also advances in representation, especially in how to represent independence or irrelevance in the light of imprecision [Coz00]. Accounts of such early developments can be found in the surveys by Cano [CM00] and Cozman [Coz05].
Recent advances
The last decade witnessed a significant progress on the study of computational complexity of inference and decision making with credal networks, with many new algorithms proposed, and a much broader understanding of the effect of specification languages on computational complexity. We now know quite a bit about these topics: there are algorithms based on algebraic message passing and algorithms based on multilinear programming (some of which lead to integer programming formulations); there are results on the complexity of marginal inference for several classes of credal networks, as well as some results on the complexity of decision making. A larger number of successful applications of credal networks in many specialist domains have appeared during the last decade or so, from machine learning tasks to engineering to medical diagnosis.
The interested reader can benefit from a number of surveys and tutorials that have been published throughout the years:
- An early account of the theory of credal networks, and in particular of algorithms then used to deal with them, can be found in the survey Algorithms for imprecise probabilities, published in 2000 by Cano and Moral [CM00].
- A rather broad overview of graph-theoretical tools to represent and manipulate imprecise/indeterminate probabilities, as they were available in 2005, is available in Graphical models for imprecise probabilities by Cozman [Coz05]. That survey tried to capture all that was known about credal networks at that time: different extensions (strong and epistemic), algorithms, and connections with Bayesian networks.
- A detailed tutorial on how to build credal networks, up to the construction of real knowledge-based systems, is delivered by Piatti, Antonucci and Zaffalon in Building knowledge-based systems by credal networks: A tutorial [PAZ10].
- A rather gentle introduction to credal networks can be found in Probabilistic graphical models, published in 2014 by Antonucci, de Campos and Zaffalon as a chapter in a popular book on imprecise probabilities [ACZ14]. This piece offers probably the best path for the novice to get acquainted with credal networks, as well as a reference point for everyone interested in the topic.
- An authoritative discussion of epistemic extensions of credal networks can be found in De Bock’s piece on Credal networks under epistemic independence [De 17], a mandatory text for the more advanced reader, in particular the one interested in epistemic independence.
- An updated survey of the theory of credal networks, with particular emphasis on strong extension, is the theme of Thirty years of credal networks: Specification, algorithms and complexity, published by Mauá and Cozman in 2020 [MC20]. The present text is an abridged version of that paper; there the reader will find a comprehensive view of the theory, with many different characterizations of the semantics of such models, and their consequences on inference and decision making. The survey was written such that it serves from the newcomer being introduced to the theory of constructing reliable decision making systems, to the more experienced researcher that desires an up-to-date review of more recent advances.
Main references
[SB75] E. H. Shortliffe and B. G. Buchanan. “A model of inexact reasoning in medicine”. In: Mathematical Biosciences 23 (1975), pp. 351-379.
[Qui82] J. R. Quinlan. INFERNO: A Cautious Approach to Uncertain Inference. Technical report N-1898-RC. RAND Corporation, 1982.
[Nil86] N. J. Nilsson. “Probabilistic logic”. In: Artificial Intelligence 28.1 (1986), pp. 71-87.
[Pea86] J. Pearl. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann, 1988.
[LM90] M. T. Lamata and S. Moral. “Dependence Graphs: Upper and Lower Probabilities”. In: System Analysis and Computer Science. 1990, pp. 113-122.
[Wal91] P.Walley. Statistical Reasoning with Imprecise Probabilities. Chapman and Hall, 1991.
[Tes92] B. Tessem. “Interval probability propagation”. In: International Journal of Approximate Reasoning 7.3-4 (1992), pp. 95-120.
[CDM93] J. Cano, M. Delgado and S. Moral. “An Axiomatic Framework for Propagating Uncertainty in Directed Acyclic Networks”. In: International Journal of Approximate Reasoning 8 (1993), pp. 253-280.
[FZ98] E. Fagiuoli and M. Zaffalon. “2U: An Exact Interval Propagation Algorithm for Polytrees with Binary Variables”. In: Artificial Intelligence 106.1 (1998), pp. 77-107.
[CM00] A. Cano and S. Moral. “Algorithms for imprecise probabilities”. In: Handbook of Defeasible and Uncertainty Management Systems. Ed. by J. Kohlas and S. Moral. Kluwer Academic Publishers, 2000, pp. 369-420.
[Coz00] F. G. Cozman. “Credal networks”. In: Artificial Intelligence 120.2 (2000), pp. 199-233.
[Coz05] F. G. Cozman. “Graphical models for imprecise probabilities”. In: International Journal of Approximate Reasoning 39.2-3 (2005), pp. 167-184.
[Dar09] A. Darwiche. Modeling and Reasoning with Bayesian Networks. Cambridge University Press, 2009.
[KF09] D. Koller and N. Friedman. Probabilistic Graphical Models. MIT press, 2009.
[PAZ10] A. Piatti, A. Antonucci and M. Zaffalon. “Building Knowledge-Based Systems by Credal Networks: A Tutorial”. In: Advances in Mathematics Research 11. Nova Science, 2010, pp. 227-279.
[ACZ14] A. Antonucci, C.P. de Campos and M. Za alon. “Probabilistic graphical models”. In: Introduction to Imprecise Probabilities. Edited by Thomas Augustin et al. Wiley, 2014. Chapter 9, pp. 207-229.
[Ken14] S. Kent. Words of Estimative Probability. In Sherman Kent and the Board of National Estimates: Collected Essays. Historical Document (online). 2014.
[De 17] J. De Bock. “Credal networks under epistemic irrelevance”. In: International Journal of Approximate Reasoning 85 (2017), pp. 107-138.
[MC20] D. D. Mauá and F. G. Cozman. “Thirty years of credal networks: Specification, algorithms and complexity”. In: International Journal of Approximate Reasoning 126 (2020), pp. 133-157.

