Ignacio Montes’ PhD thesis on Comparison of alternatives under Uncertainty and imprecision

Posted on June 24, 2014 by Ignacio Montes
[ go back to blog ]

This thesis, supervised by Enrique Miranda and Susana Montes, was defended on May 16th. The jury was composed of Susana Díaz, Serafín Moral and Bernard De Baets.

Summary

This thesis deals with the problem of comparing alternatives defined under some lack of information, that is considered to be either uncertainty, imprecision or both together.

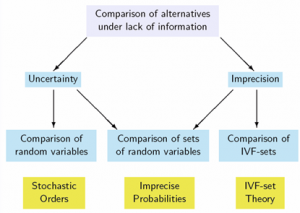
• Alternatives defined under uncertainty are modeled by means of random variables, and therefore they are compared using stochastic orders [4].
• When the alternatives are defined under both uncertainty and imprecision, they are modeled by means of sets of random variables, and tools of the Imprecise Probability Theory [7] are used.
• When the alternatives to be compared are defined under imprecision, but without uncertainty, they can be modeled using fuzzy sets or any of its extensions, like for instance Atanassov Intuitionistic Fuzzy Sets [1].

Comparison of random variables

Stochastic orders are methods that allow the comparison of random quantities. In this thesis we have focused on stochastic dominance and statistical preference, two stochastic orders that possess totally different interpretations. The former is based on the direct comparison of the cumulative distribution functions associated with the random variables, so it only uses marginal information, while the latter is based on a probabilistic relation providing preference degrees and using the joint distribution.

Although these stochastic orders are not related in general, we have found conditions under which stochastic dominance implies statistical preference. These conditions are based on the type of variables and the copula [5] that links them: independent random variables, simple or continuous and comonotone random variables, simple or continuous and countermonotone random variables or continuous random variables coupled by an Archimedean copula.

Both stochastic dominance and statistical preference are intended for the pairwise comparison of random variables. The reason is that stochastic dominance imposes a too strong condition for comparing three (or more) cumulative distribution functions (they must be ordered!)  and statistical preference does not prevent the existence of cycles, that is, it is not transitive [2]. For this reason we have proposed an extension of statistical preference for the comparison of more than two random variables at the same time. It preserves the same advantages than the pairwise statistical preference: it is a complete order, it provides degrees of preference, so the greater the degree the most preferred is the variable, and it uses all the available information because it is based on the joint distribution of all the random variables. Furthermore, we have shown that this general statistical preference can be applied to decision making problems with linguistic labels.

Comparison of sets of random variables

When the alternatives are defined under both uncertainty and imprecision, they are modeled by means of sets of random variables with an epistemic interpretation, meaning that all we know about the real (but unknown) random variable is that it belongs to the set.

In this framework, the first thing we have done is to extend stochastic orders to the comparison of sets of random variables instead of single ones. Any stochastic order has been extended in six different ways, and some of the choice between these extensions depends on the given interpretation (pessimistic or optimistic). We have seen that when the stochastic order to be extended is the expected utility, our six extensions are quite related to some usual criteria of the decision making with imprecise probabilities [6], such as interval dominance, maximax or maximin criteria,…

When the stochastic order to be extended is stochastic dominance, the comparison of the set of random variables is made by means of the comparison of their associated sets of cumulative distribution functions. In this sense, since each set of cumulative distribution functions can be summarized by means of its associated p-box, we have seen that there is a strong connection between the six extensions of stochastic dominance and the comparison of the bounds of the associated p-boxes by means of the stochastic dominance. Finally, when we extend statistical preference, the extensions are related to the comparison of the lower or upper medians of the adequate set of random variables.

Our general approach can be applied to three particular situations:

1. When we want to compare belief functions, we can consider their associated credal sets, and apply there our six extensions of stochastic dominance. In this framework, our six extensions give rise to the four possibilities considered by Denouex in [3] for the comparison of belief functions with respect to stochastic dominance.

2. When we want to compare random variables with imprecise utilities, we can consider random sets modeling our lack of information. Then, since we are using an epistemic interpretation, all we know about the real (but unknown) random variables is that they belong to the sets of measurable selections. Thus, in order to compare the random sets we can compare their sets of measurable selections by means of the extension of the adequate stochastic order.

3. When we want to compare random variables and we have imprecise knowledge about the probability of the initial space, we can consider a credal set. In this situation, any random variable defines a set of random variables formed by the combinations of the random variable with the different probabilities in the credal set.

Next step was to investigate how to perform the comparison of random variables with imprecise joint distribution. In this situation we use p-boxes and bivariate p-boxes to model the imprecise knowledge about the marginal and joint distribution functions, respectively, and we use sets of copulas, whose information is summarized by an imprecise copula, to model the unknown copula. Sklar’s Theorem [5] is a well-known result on Probability Theory that allows expressing the joint distribution function in terms of the marginals. However, when there is imprecision about the joint (or the marginals) distribution function, it cannot be applied. For this reason, we have extended Sklar’s Theorem to an imprecise setting. This result has shown to be very useful in two situations:

1. When we have two marginal p-boxes and we want to compute their natural extension, we can apply the imprecise Sklar Theorem to the marginal with the imprecise copula determined by Lukasiewicz’s and  minimum copulas.

2. When we want to compute the strong product of the marginal p-boxes, we can apply the imprecise Sklar Theorem to the marginals with the product copula.

Comparison of intuitionistic fuzzy sets

Finally, when the alternatives to be compared are defined under imprecision, but without uncertainty, they can be modeled using fuzzy sets or any of its extensions, like for instance Atanassov Intuitionistic Fuzzy Sets (AIFS, for short). Several measures of comparison of this kind of sets can be found in the literature, and they are classified into two main families: distances and dissimilarities. This thesis introduces a new family of measures of comparison of AIFS: divergences, that impose stronger conditions than dissimilarities. We have also seen that these three measures can be included in a more general measure of comparison of AIFS, in the sense that depending on the required conditions, we may obtain a distance, a dissimilarity or a divergence.

A particular type of divergences, those satisfying a local property, is studied in detail, shown to have interesting properties, and applied to decision making and pattern recognition.

Conclusions

The main contributions of this thesis can be summarized as follows:

• Investigation of the properties of stochastic dominance and statistical preference. In particular, study of conditions under which both are related.
• Extension of statistical preference for the comparison of more than two random variables simultaneously.
• Extension of stochastic orders to the comparison of sets of random variables instead of single ones.
• Particular cases: imprecise stochastic dominance, related to the comparison of bounds of p-boxes, and imprecise statistical preference, related to the comparison of lower and upper medians.
• The definitions introduced by Denoeux are included as particular case of our more general approach.
• Two particular situations in decision making: comparison of random variables with imprecise utilities and beliefs.
• Imprecise version of Sklar’s Theorem.
• Divergences as a new measure of comparison of AIFS.
• Local divergences applied to decision making and pattern recognition.

Basic references

[1] K. Atanassov. Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 20:87-96, 1986.

[2] B. De Schuymer, H. De Meyer, B. De Baets. A fuzzy approach to stochastic dominance of random variables. Lecture Notes in Artificial Intelligence 2715, 253-260, 2003.

[3] T. Denoeux. Extending stochastic ordering to belief functions on the real line. Information Sciences, 179: 1362-1376.

[4] A. Müller and D. Stoyan. Comparison Methods for Stochastic Models and Risks. Wiley, 2002.

[5] R. Nelsen. An introduction to copulas. Springer, New York, 1999.

[6] M. C. M. Troffaes. Decision making under uncertainty using imprecise probabilities. International Journal of Approximate Reasoning, 45(1):17-29, 2007.

[7] P. Walley. Statistical reasoning with imprecise probabilities. Chapman and Hall, London, 1991.

About the author

Ignacio Montes started his PhD in the UNIMODE Research Unit in 2010 with a grant of the Spanish Ministry of Science. He is currently a member of the Dep. of Statistics and O.R of the University of Oviedo, Spain.